
La Η σύνθεση στη φωτογραφία είναι μια από τις ιδιότητες που πρέπει να έχει κάθε φωτογράφος επαγγελματίας που καυχιέται γι 'αυτό. Υπάρχουν μια σειρά κανόνων που βοηθούν στη σύνθεση αυτής της σκηνής ή στη σύλληψη εκείνης της στιγμής κατά την οποία μια σειρά περιστάσεων ενώνονται, έτσι ώστε, χάρη στο ειδικό μάτι μας, μπορούμε να τραβήξουμε μια φωτογραφία που μας οδηγεί σε μια φωτογραφία όμορφης κατασκευής.
Ενας από αυτούς Ο κανόνας είναι αυτός των τρίτων ή που μπορεί επίσης να ονομαστεί χρυσός λόγος. Και δεν είναι τρόπος κατανόησης της τοποθέτησης μιας σειράς στοιχείων σε μια φωτογραφία που γεννήθηκε πριν από χρόνια, αλλά μάλλον πριν από αιώνες. Είναι ο Λεονάρντο Πισάνο, επίσης γνωστό ως Fibonacci, ο οποίος αποκάλυψε αυτόν τον κανόνα, ο οποίος εκείνη την εποχή αυτός ο Ιταλός μαθηματικός ονόμασε τη διαδοχή Fibonnaci, και που σήμερα γνωρίζουμε ως χρυσή αναλογία.
Ποια είναι η χρυσή αναλογία;
Πραγματικά είναι μια σειρά αριθμών: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 κ.λπ.. Είναι μια άπειρη σειρά στην οποία το άθροισμα των δύο αριθμών που βρίσκονται διαδοχικά, θα οδηγεί πάντα στον επόμενο αριθμό. Δηλαδή, 1 + 1 = 2; 2 + 13 = 3 και ούτω καθεξής. Μεταξύ των δύο διαδοχικών αριθμών υπάρχει μια σχέση που είναι κοντά σε αυτό που είναι ο χρυσός αριθμός, ή 1,168034, ακριβώς ποιο θα ήταν το γράμμα Phi του ελληνικού αλφαβήτου.

Όπως λένε πολλοί, τα μαθηματικά είναι τα πάντα και αξίζει να αναρωτηθούμε τι χρησιμεύουν αυτοί οι λογαριασμοί για την εφαρμογή τους στην τέχνη. Θα πρέπει να αντιμετωπίσουμε ένα ορθογώνιο στο οποίο οι πλευρές του μετρούν δύο από τους αριθμούς στη σειρά Fibonacci.
Αυτό που πρέπει να κάνουμε είναι διαιρέστε τους δύο αριθμούς στις πλευρές για να διαιρέσετε το ορθογώνιο και θα ήταν ως εξής:
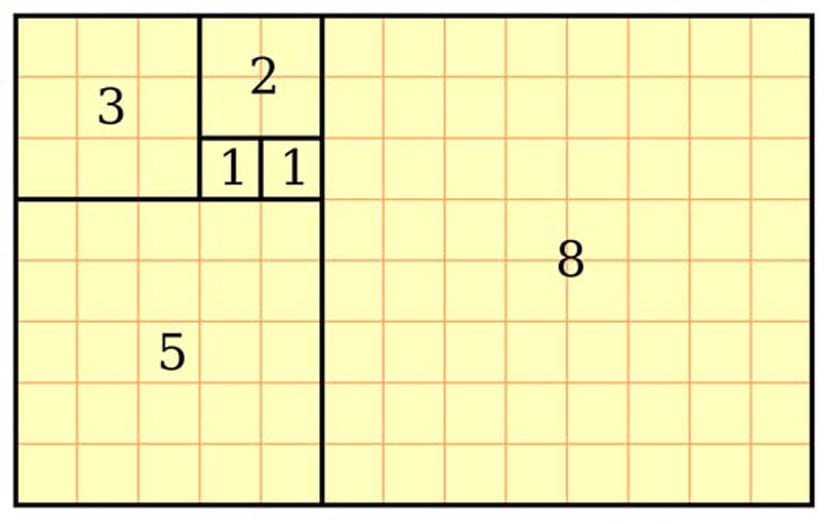
Εμείς μόνο Θα ήταν απαραίτητο να σχεδιάσουμε μια γραμμή που συνδέει όλα αυτά τα μικρά τετράγωνα. Είναι αυτή η σπείρα που ονομάζεται Χρυσή Σπείρα ή Χρυσή Σπείρα, και με πολύ περίεργο τρόπο μπορούμε να την βρούμε με πολλούς τρόπους στη φύση. Απλώς πρέπει να ρίξουμε μια ματιά γύρω μας και θα δούμε ότι οι σπόροι ενός ηλίανθου ακολουθούν τις γραμμές της Χρυσής Σπείρας κατάπληξη.
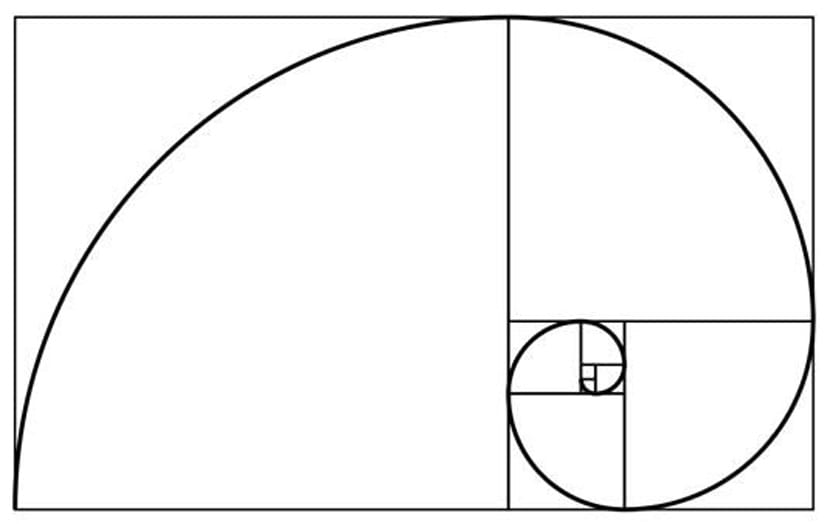
Και εδώ μπαίνουμε στην ιδέα αυτής της σπείρας για να την εφαρμόσουμε σε όλα τα είδη καλλιτεχνικών μορφών. Όντας οπτικά φυσικές αναλογίες, οι εικόνες που συντίθενται με αυτήν τη σπειροειδή γραμμή θα είναι ικανός να τραβήξει την προσοχή του θεατή. Και όπως κάθε καλλιτεχνικός κλάδος, δεν πρέπει ποτέ να υπόκεινται σε αυτόν τον κανόνα, ο οποίος μπορεί να παραβιαστεί, αλλά χρησιμεύει ως οδηγός για να ξεκινήσετε μια δουλειά, πάντα ανοιχτή σε τροποποιήσεις που πιστεύουμε ότι μπορεί να είναι χρήσιμες.
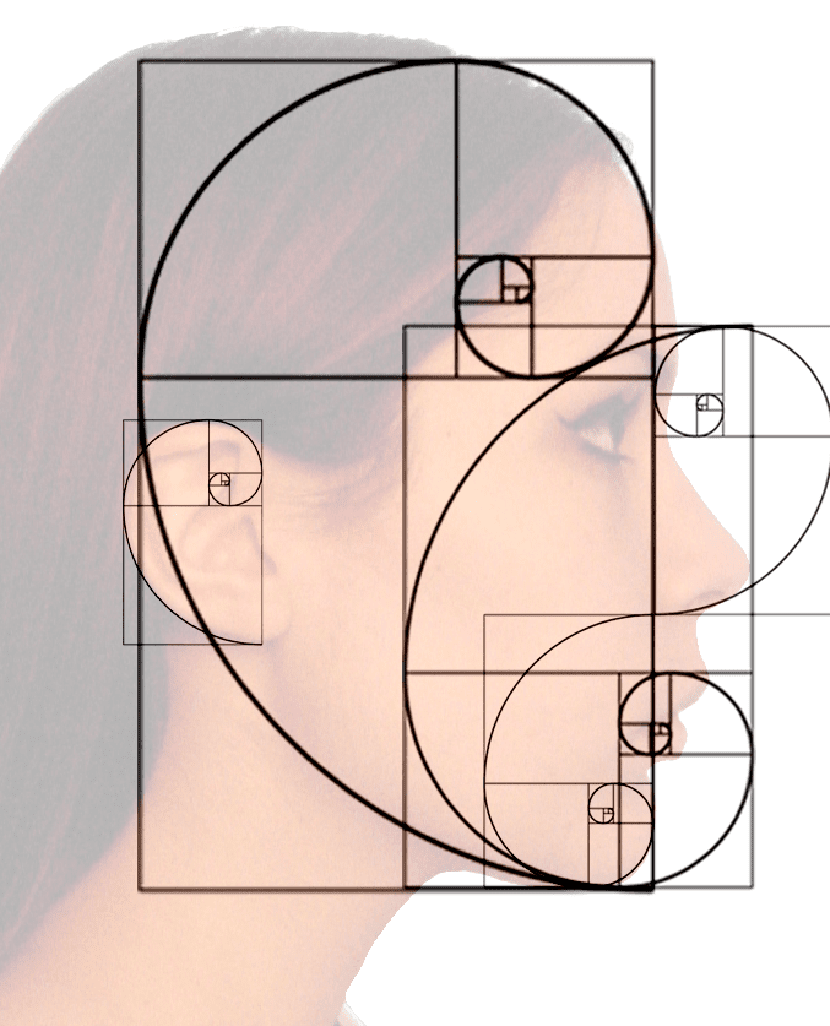
Η "Χρυσή αναλογία", όπως ονομάζεται στα Αγγλικά, είναι περίπου σε αναλογία ίσο με 1: 1.61 και μπορούμε να το αναπαραστήσουμε με το "χρυσό ορθογώνιο", το οποίο αποτελείται από ένα τετράγωνο και ένα μικρότερο ορθογώνιο. Εάν αφαιρέσουμε το τετράγωνο από το ορθογώνιο, θα μείνουμε με ένα άλλο "χρυσό ορθογώνιο". Αυτά τα βήματα θα μπορούσαν να συνεχιστούν απεριόριστα, όπως και με τους αριθμούς Fibonacci, οι οποίοι λειτουργούν αντίστροφα.
Η ιστορία της Χρυσής Αναλογίας
Πρεπει να επιστρέψτε τουλάχιστον πριν από 4.000 χρόνια όταν άρχισε να χρησιμοποιείται το Golden Ratio. Και είναι ότι ακόμη και μερικοί ιστορικοί επιστρέφουν στους αρχαίους Αιγύπτιους, οι οποίοι έχουν ήδη χρησιμοποιήσει αυτήν την αρχή για την κατασκευή των πυραμίδων. Προς το παρόν μπορούμε να το βρούμε σε όλες τις πτυχές της τέχνης, από τη μουσική, το σχεδιασμό ή την απεικόνιση. Εφαρμόζοντας αυτήν τη μεθοδολογία εργασίας, μπορείτε να φέρετε τις ίδιες ευαισθησίες στο δικό σας έργο.
Στην ελληνική αρχιτεκτονική

Στην ελληνική αρχιτεκτονική Αυτή η αναλογία χρησιμοποιήθηκε για τον προσδιορισμό της τέλειας αρμονίας και σχέσης μεταξύ του πλάτους ενός κτιρίου και του ύψους του, του μεγέθους της στοάς και ακόμη και της θέσης των στηλών, εκείνων που υποστηρίζουν όλο το βάρος και την ίδια τη δομή.
Το τελευταίο δείπνο

Ο μεγάλος Λεονάρντο ντα Βίντσι, όπως και άλλοι καλλιτέχνες πολλών εποχών, χρησιμοποίησε την "χρυσή αναλογία" σε αυτό το γνωστό έργο. Οι μορφές που χαρακτηρίζουν τη σύνθεση είναι μικρότερες από τα δύο τρίτα, και η θέση του Ιησού βρίσκεται τέλεια ώστε να ταιριάζει στη χρυσή αναλογία ολόκληρου του καμβά.
Παντού

La Η φύση χρησιμοποιεί αυτήν τη χρυσή αναλογία ως δικό της σύμβολο πόσο καθολική έχει αυτή η μεθοδολογία. Μπορούμε να το δούμε παντού, όπως δείχνει το βίντεο, όπως σε λουλούδια, λιβελλούλες ή όστρακα.
Η διαδικασία δημιουργίας ενός ορθογωνίου με το Golden Ratio
- Το πρώτο πράγμα είναι να σχεδιάσετε ένα τετράγωνο.

- Το επόμενο πράγμα είναι να το χωρίσουμε σε δύο.
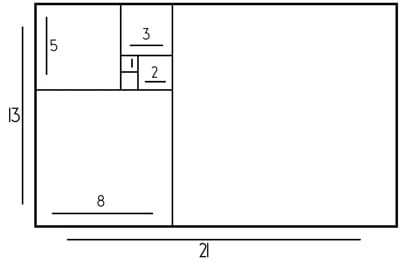
- Se σχεδιάστε μια διαγώνια από μία από τις κεντρικές γωνίες, το ένα παρακάτω, στο άλλο στην αντίθετη γωνία.
- Περιστρέφουμε τη διαγώνια έτσι ώστε να εμφανίζεται οριζόντια δίπλα στο πρώτο ορθογώνιο.
- Δημιουργούμε ένα ορθογώνιο από τη νέα οριζόντια γραμμή και ακολουθήστε το οριζόντιο ορθογώνιο.
Χρήση του ορθογωνίου που δημιουργήθηκε
Ο κανόνας των τρίτων μας οδηγεί να χωρίσουμε μια περιοχή σε τρία ίσα μέρη, κάθετα και οριζόντια. Είναι η τομή των γραμμών που προτείνουν ένα φυσικό σημείο εστίασης για το σχήμα. Και είναι οι καλλιτέχνες ή οι φωτογράφοι που τοποθετούν το βασικό στοιχείο της σύνθεσής τους σε μια από αυτές τις τεμνόμενες γραμμές για να δημιουργήσουν αυτή τη σκηνή που είναι πιο ευχάριστη για τον θεατή.

Αυτή η μεθοδολογία μπορεί να είναι χρησιμοποιείται στο οπτικό στυλ των ιστοσελίδων, κοροϊδεύω και σχέδια αφισών ή διαφήμιση. Εάν ήδη χρησιμοποιούμε τον κανόνα των τρίτων προς τις χρυσές αναλογίες, που είναι 1: 1.6, θα είμαστε πολύ κοντά στο χρυσό ορθογώνιο, το οποίο θα κάνει το όραμά σας ακόμη πιο ευχάριστο.
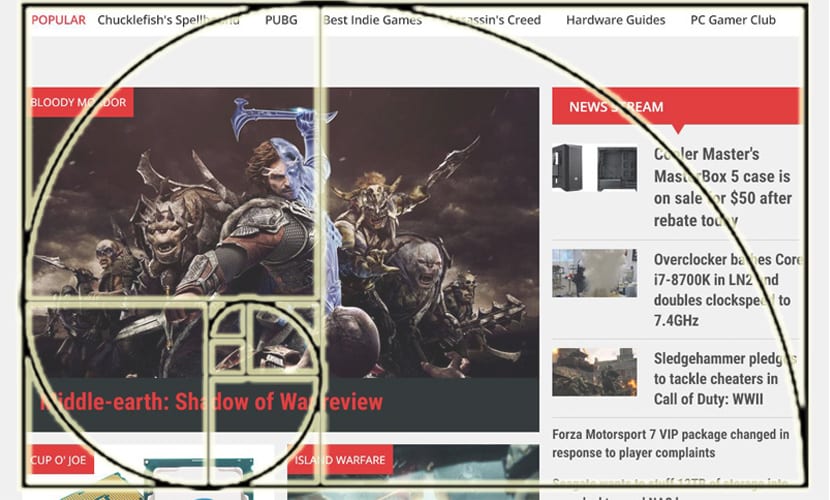
Στο web design έχουμε ένα εντυπωσιακό παράδειγμα και στο οποίο έχουμε συνηθίσει. Από τη μία πλευρά έχουμε όλες τις προσβάσεις σε widget και μενού, ενώ στην άλλη πλευρά, το μεγαλύτερο τετράγωνο, είναι ιδανικό για το περιεχόμενο. Εάν είχαμε μια περιοχή περιεχομένου 640 pixel, η πλευρά των 400 pixel θα ταιριάζει απόλυτα στο Golden Ratio. Μπορούμε πάντα να χρησιμοποιούμε την ίδια διαίρεση στα τετράγωνα σχεδόν απεριόριστα, αρκεί να τα βλέπουμε χωρίς να χρειάζεται να τεντώσουμε τα μάτια μας.
Περιέργειες σχετικά με τη χρυσή αναλογία
- Η ακολουθία Fibonacci, αριθμητικός συγγενής του χρυσού αριθμού, έχει μια αρκετά εντυπωσιακή περιέργεια και είναι σχετίζεται με την αναπαραγωγή κουνελιών που εκτρέφονται από τον ίδιο τον Leonardo Pisano Bionacci στο βιβλίο του για τον άβακα το 1202.

¿Πόσα ζεύγη κουνελιών θα έχουμε στο τέλος του έτουςΕάν ξεκινήσουμε με ένα ζευγάρι που παράγει ένα άλλο κάθε μήνα και που δημιουργεί σε ηλικία δύο μηνών; Η απάντηση από μήνα σε μήνα είναι: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 και 144.
- Ο χρυσός αριθμός συναρπάζει γιατί είναι μπορεί να βρεθεί φυσικά στη φύση, όπως συμβαίνει μεταξύ των θηλυκών και των βαμμένων μελισσών, οι οποίες σε μια κυψέλη έχουν συνήθως αυτή τη χρυσή αναλογία.
- Μια άλλη περιέργεια, και σχετίζεται με το ανθρώπινο σώμα, είναι η ικανότητα προσδιορισμού εάν η μήτρα ενός ασθενούς φαίνεται φυσιολογική όταν χρησιμοποιεί τη χρυσή αναλογία. Το ύψος του διαιρείται με το πλάτος του, έτσι ώστε το αποτέλεσμα να είναι κοντά στο 1,618.
- Αν κοιτάξουμε την τέχνη, μέσα στο κυβιστικό κίνημα, υπάρχει ένα χρυσό τμήμα. Το επίκεντρο ήταν να φέρει τα μαθηματικά στη ζωγραφική, και η ιδέα ήταν να αποσυντεθούν οι μορφές σε κύβους. Ένας από τους καλλιτέχνες που σχετίζονται με αυτήν την ενότητα ήταν ο Marcel Duchamp, αν και έχουμε επίσης τον υπέροχο Juan Gris.

- Ένα άλλο μεγάλο Ο Antonio Stradivarius χρησιμοποίησε τη χρυσή αναλογία για να τοποθετήσει τα ανοίγματα στα βιολιά του να είναι ισοδύναμοι με αυτόν τον αριθμό. Αυτό που είναι άγνωστο είναι αν η κατάσταση των ανοιγμάτων είχε σχέση με την ποιότητα του ήχου, αν και φαίνεται να είναι πιο αισθητικό.
- Τελειώνουμε με μια άλλη περιέργεια και πηγαίνουμε απευθείας με το χρηματιστήριο και τις χρηματιστηριακές αξίες. Μεταξύ των εργαλείων που χρησιμοποιούν οι αναλυτές για να ενσωματώσουν τη συμπεριφορά μιας ασφάλειας, είναι οι προβολές Fibonacci. Χρησιμοποιούνται για τη σήμανση των επιπέδων και έτσι γνωρίζουν και τα δύο ριμπάουντ ως κατάντη.
Εργαλεία Ιστού για το Golden Ratio
Υπολογιστής τυπογραφίας Golden Ratio
Αντιμετωπίζουμε ένα διαδικτυακό εργαλείο που σας επιτρέπει να ανακαλύψετε ποια είναι η τέλεια γραμματοσειρά για τον ιστότοπό μας. Πρέπει απλώς να εισαγάγουμε το μέγεθος της γραμματοσειράς και το πλάτος του περιεχομένου και ως εκ τούτου θα έχουμε την τέλεια αναλογία για την τυπογραφία.
Μια άλλη από τις αξίες της είναι η ικανότητα να βελτιστοποίηση της τυπογραφίας με βάση το μέγεθος της γραμματοσειράς, ύψος γραμμής, πλάτος και χαρακτήρες ανά γραμμή, οπότε είναι από μόνη της ένα πολύτιμο εργαλείο για να δώσει αυτό το άγγιγμα στον ιστότοπό μας, εάν είμαστε προγραμματιστές.
Μπορούμε να χρησιμοποιήσουμε απλά εισάγοντας το μέγεθος της γραμματοσειράς, το πλάτος του περιεχομένου ή και τα δύο. Μπορούμε επίσης να εισαγάγουμε την τιμή CPL και θα μας δώσουν τιμές για τη βελτιστοποίηση των χαρακτήρων ανά γραμμή. Μια ενδιαφέρουσα εφαρμογή για να εκμεταλλευτείτε πλήρως τη χρυσή αναλογία για ανάπτυξη ιστοσελίδων.
Φυσική αριθμομηχανή

Με το Phicalculator αντιμετωπίζουμε ένα widget για Mac OSX που έδωσε έναν αριθμό, θα είναι σε θέση να υπολογίσει την τιμή αντιστοιχεί κατά τη χρήση του χρυσού λόγου. Είναι ένας υπολογιστής για αυτό το ευρετήριο που θα ισχύει για κάθε τύπο εργασίας που πρόκειται να κάνουμε. Δηλαδή, εισάγουμε οποιονδήποτε αριθμό και παρακάτω θα έχουμε το αποτέλεσμα με τη χρυσή αναλογία. Δεν μπορεί να είναι ευκολότερο.
Atrise Golden Τμήμα
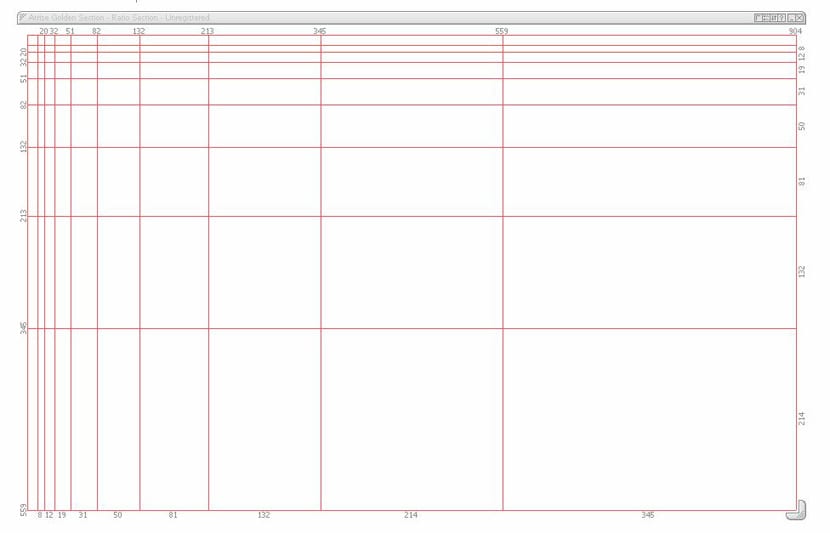
Ένα άλλο πρόγραμμα που λειτουργεί τέλεια ως εργαλείο σχεδίασης για καλλιτέχνες, σχεδιαστές, προγραμματιστές και φωτογράφους. Σε αντίθεση με τα προηγούμενα δύο εργαλεία ιστού, εδώ θα πρέπει να κατεβάσουμε τη δωρεάν δοκιμή 30 ημερών ή να την αγοράσουμε απευθείας.
Μπορεί να χρησιμοποιηθεί με οποιοδήποτε πρόγραμμα σχεδίασης και χαρακτηρίζεται από βρείτε τις τέλειες διαστάσεις και σχήματα για να πάρετε το καλύτερο πλαίσιο από μια φωτογραφία, για παράδειγμα. Είναι διαθέσιμο τόσο για Windows όσο και για Mac OS.
Εξαιρετική συλλογή. Ευχαριστώ.